Synthesizer
Overview
MuseScore's synthesizer creates audio using the sample-based synthesis(wikipedia) and virtual instrument technology. MuseScore 3 comes with the free MuseScore_General.sf3 sound library (sample library) file, see the SoundFonts and SFZ files chapter.
Clicking on top toolbar's play button, or exporting an audio file etc instructs Musescore 3.6.2 to uses the current program session synthesizer settings. The Synthesizer window contains these settings, they include:
- The sound libraries used. To use a custom sound library, it must be installed onto the machine first, see the SoundFonts and SFZ files chapter.
- The post-processing effects such as reverb and compression.
- The master tuning. For note-level tuning, edit a note's Tuning property in the Inspector.
- The overall output volume. For instrument-level controls, see the Mixer chapter.
- The master Midi Continuous Controllers (MIDI CC) setting (versions 3.1 and above). For staff-level override, see the Staff / Part properties chapter.
To display the Synthesizer window, select View→Synthesizer. It has the following tabs:
- Fluid: SF2/SF3 files configuration.
- Zerberus: SFZ files configuration.
- Master Effects: Post-processing effect configuration.
- Tuning: The master tuning configuration.
- Dynamics (versions 3.1 and above): The master MIDI CC configuration.
Synthesizer settings
The Synthesizer window contains settings that Musescore uses during the current program session. Settings can be saved into and loaded from two types of places:
- The operating system, also known as the "default" profile,
- Score files such as *.mscz and *.mscx.
Auto and manual loading
Clicking on top toolbar's play button, or exporting an audio file etc instructs Musescore 3.6.2 to uses these current program session synthesizer settings. The synthesizer settings data existed in the score file (if any) are not used.
The only time any synthesizer settings are automatically loaded is when the user opens the Musescore program. During program startup, the synthesizer settings saved on the operating system (the "default" profile) are loaded.
Opening a score file does not automatically load its synthesizer settings data inside into the current session. Also, in the case of multiple opened score files in one program session, switching to view another score does not automatically update the current session synthesizer settings to those data saved inside the score file.
Auto and manual saving
Changed settings are never automatically saved. User must uses the buttons at the bottom of the Synthesizer window.
Save and load buttons
Use the buttons at the bottom of the Synthesizer window to manage settings under all tabs (see overview):
| Button | Function |
|---|---|
| Set as Default | Saves the current synthesizer settings into the operating system (the "default" profile). The "default" profile will be automatically loaded during MuseScore startup next time. Subsequent changes in the synthesizer window are not automatically saved into the operating system (the "default" profile). |
| Load Default | Loads the last saved synthesizer settings inside the operating system (the "default" profile) into the current session. |
| Save to Score | Saves the current synthesizer settings into the score file that the user is currently viewing only, but not into other opened score files. The score file synthesizer setting data is never automatically loaded or utilized directly. |
| Load from Score | Loads the synthesizer settings data existed inside the score file (if any) into the current session. |
Ordering of the sound libraries
When arranging the sound libraries to the list under Fluid tab or Zerberus tab, keep in mind that the order of sound libraries affects audio generation:
- If the score file is using default Musescore instruments (see the Instruments chapter), Musescore only creates correct audio if the built-in MuseScore_General.sf3 is the 1st ordered item.
- When a new sound library is added into the list, it is inserted as the 1st ordered item, user may need to rearrange the list.
- After manually changing Sound property in the Mixer window and achieving a desired audio output, user should save the current sound library ordering so that it can be retrieved later.
- When the user restarts Musescore, sound libraries ordering may changes or reset, as explained in the "synthesizer settings" session above.
Fluid (SF2/SF3)
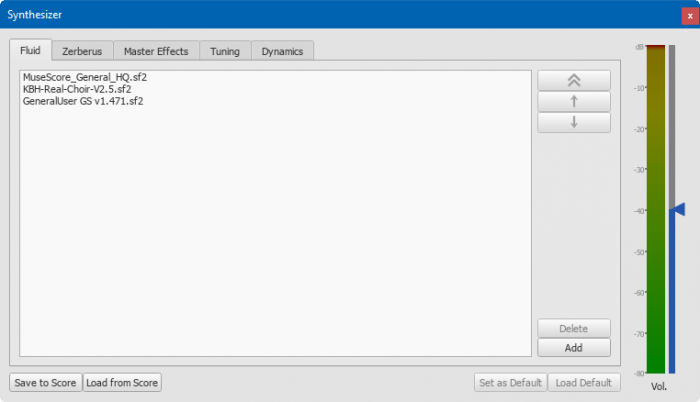
The Fluid tab allows users to load, rearrange or disable SF2 and SF3 files for the current session for playback and audio export purpose. By default, the list shown one and only one item, the built-in MuseScore_General.sf3. To use a custom sound library, it must be installed onto the machine first, see the SoundFonts and SFZ files chapter.
Using a new SF2/SF3 in the current session
- Make sure the SF2/SF3 is installed.
- Click on the Add button
- Select the SF2/SF3 file.
Reordering the SF2/SF3s
- Click on an item on the list
- Use the up/down arrows (on the right-hand side) to adjust the order.
- Repeat if required.
- Or use the double up arrow (on the top right-hand side) to move any item to the top of the list.
NOTE: Reordering SF2/SF3 is usually unneccessary, as explained in the "Ordering of the sound libraries" session.
Disabling a SF2/SF3 for the current session
- Click on an item on the list
- Click on the Delete button.
NOTE: Disabling SF2/SF3 is usually unneccessary. Disabling a higher ordered item changes the list's ordering and affects playback of Musescore instruments that utilize lower ordered items, as explained in the "Ordering of the sound libraries" session.
Zerberus (SFZ)
The Zerberus tab allows users to load, rearrange or disable SFZ files for the current session in a similar way to SF2/SF3 in the Fluid tab.
Effects
The Master Effects tab allows user to add and adjust reverb and compression post-processing effect.
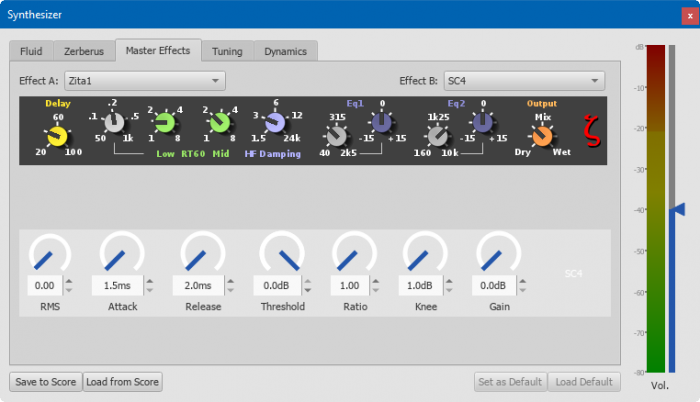
Master Effects with Zita1 Reverb and SC4 Compressor.
To turn an effect on or off:
- Select an option from the drop-down list next to Effect A or Effect B (the effects are applied in series, A → B).
To store and load effects configurations, use the buttons at the bottom of the Synthesizer window. See Synthesizer settings (above) for details.
Zita 1 reverb
The Zita 1 stereo reverb module allows you to simulate the ambience of anything from a small room to a large hall. The pre-delay, reverb time and tone of the reverb can be finely tuned using the controls provided:
- Delay: Set a pre-delay for the reverb from 20-100 ms.
- Low RT60 (Low frequency reverb time): Use the grey control to adjust the center frequency (50–1000 Hz) of the low frequency band which you want to affect: the green control adjusts the reverb time (1–8 secs) of this frequency band.
- Mid RT60 (Mid-range reverb time): Adjust the reverb time (1–8 secs) of the mid-range frequency band.
- HF Damping: Adjusts the high frequency component of the reverb. Increasing this value increases the frequency of the cut-off point and makes the reverb appear brighter and longer.
- EQ1: Allows you to cut or boost (-15 to +15) a frequency band (center = 40 Hz - 2 KHz) in the lower part of the spectrum.
- EQ2: Allows you to cut or boost (-15 to +15) a frequency band (center = 160 Hz - 10 KHz) in the higher part of the spectrum.
- Output: Controls the amount of effect applied. "Dry" is no effect. "Wet" indicates 100% reverb. "Mix" is a 50/50 balance of wet/dry signal.
Note: EQ1 and EQ2 affect the tone of the reverb only, not the dry (unprocessed) signal.
To quickly set up an effects patch, set "Output" to "Mix" and adjust the "Mid RT60" control to the desired reverb time. Then fine tune the effect as explained above.
SC4 compressor
The SC4 stereo compressor gives you fine control over the playback's dynamic range, reducing the volume variation between loud and soft sounds. It offers the following controls:
- RMS: Adjusts the balance between RMS (0) and Peak (1) compression. In the former, the compressor responds to averaged-out levels in the signal; in Peak mode, the compressor responds to peak levels.
- Attack: (1.5–400 ms) The length of time it takes for compression to engage fully after the signal exceeds the threshold level.
- Release: (2–800 ms) The time it takes for compression to return to zero after the signal falls below the threshold level.
- Threshold: (in dB) The signal level above which compression starts to take effect. Lowering the threshold increases the amount of signal that is compressed.
- Ratio: The amount of compression applied to the signal above the threshold. The higher the ratio, the greater the compression. Varies between 1:1 and 20:1.
- Knee: Allows you to select a range between "soft knee" and "hard knee". The softer the knee, the more gradual the transition between uncompressed and compressed signal.
- Gain: Compression tends to lower the volume, so use this control to boost the signal as required.
To quickly set-up, try setting RMS = 1, Threshold = -20 db, Ratio = 6. Increase Gain to restore the lost volume. Then fine-tune as explained above.
Tuning
The Tuning tab allows user to adjust the current session's synthesizer master tuning. To use a custom tuning system, see the Tuning systems, microtonal notation system, and playback chapter.
To change the Master tuning:
- Enter a new value in the Master tuning field, then press Change Tuning.
Dynamics (versions 3.1 and above)
Some dynamics symbols have a non-zero "Velocity change" property. When set up properly, it creates an Attack envelope simulation effect on note playback on certain instruments, eg sfz symbol on violins, see Dynamics for more information.
MuseScore also utilizes the same audio creation mechanism to simulate a variation of loudness effect on certain instruments eg crescendo on one violin long note, more info see Hairpins
This mechanism utilizes the MIDI Continuous Controller / Control Change (MIDI CC) Messages (wikipedia) technology
This tab contains settings for this audio creation mechanism. See also Different meanings of SNDs
To ensure all dynamics symbols (eg. sfz) and hairpins create correct audio on a score using the built-in MuseScore_General.sf3, use the default options.
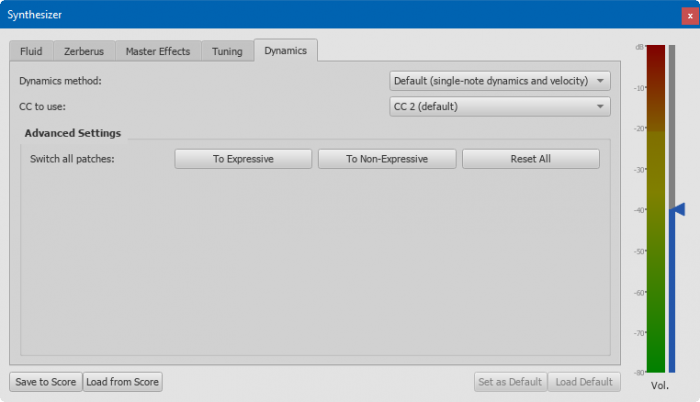
- Dynamics method: Master control
- Default (single-note dynamics and velocity): Use MIDI CC (and redundent MIDI velocity signals) to communicate with sound library if enabled in individual instrument
- Velocity only (no single-note dynamics): Ignore individual instrument's setting, use velocity only, do not use any MIDI CC
- CC events only (constant velocity): Ignore individual instrument's setting, use MIDI CC only
- CC to use:
- The MIDI CC number that Musescore use to communicate with all sound libraries. Match this to the sound libraries loaded. Users cannot edit sound library file's attenuation response inside Musescore, see Edit a Soundfont to use MIDI CC mod instead.
- Available options are CC 1, CC 2 (default), CC 4, CC 11.
- This setting is global.
- Because built-in MuseScore_General.sf3 responds CC 2, setting this to values other than CC 2 breaks playback for some dynamics symbols if the score is using a default Musescore Instrument, eg sfz symbol of default violin. See How to setup Musescore 3.x for correct playback for all dynamics and hairpins.
- Advanced Settings :
- Buttons inside this box are designed for scores using the built-in MuseScore_General.sf3. These buttons change Sound properties of all channels (track strips in the Mixer window) of every Musescore Instrument existing on the score.
- They do not affect instrument's dynamics symbol and hairpins interpretation setting 'Use single note dynamics' in Staff / Part properties
- They do not affect instruments added afterwards.
- Available options :
- To Expressive : switch to the CC 2 responsive version of sounds
- To Non-Expressive : switch to velocity responsive version of sounds
- Reset All : Reset all channels to default sound version defined in instruments.xml
Volume
The slider on the right of the Synthesizer controls the master playback volume (gain). Tread lightly, as the output volume changes dramatically with small adjustment.
See also
External links
- How to setup Musescore 3.x for correct playback for all dynamics and hairpins (MuseScore HowTo)
- Soundfont, MIDI velocity and instruments.xml (Create Musescore 3.x compatable soundfont)